Биология

Биология - Молекулярное моделирование - Молекулярная механика

09 февраля 2011


Оглавление:
1. Молекулярное моделирование
2. Молекулярная механика
3. Популярные программы для молекулярного моделирования

Молекулярная механика — один из подходов в ММ, использующий классическую механику для описания физических основ модели. Атомы представляются точечными массами с соответствующими зарядами. Взаимодействия между соседними атомами включают упругие взаимодействия и силы Ван-дер-Ваальса, описываемые традиционно потенциалом Леннарда-Джонса. Электростатические взаимодействия вычисляются по закону Кулона. Атомам в пространстве присваиваются Декартовы или внутренние координаты; в динамических расчётах атомам также могут быть присвоены скорости, соответствующие температуре. Обобщающее математическое выражение известно как потенциальная функция и соответствует внутренней энергии системы — термодинамической величине, равной сумме потенциальной энергии и кинетической. Потенциальная функция представляет потенциальную энергию как сумму энергетических членов, соответствующих отклонению от равновесных значений в длинах связей, валентных и торсионных углах, и членов для не связанных пар атомов, соответствующих ван-дер-Ваальсовым и электростатическим взаимодействиям.

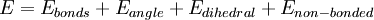
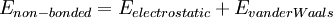
Набор параметров, состоящий из равновесных значений длин связей, валентных углов, величин парциальных зарядов, силовых констант и ван-дер-Ваальсовских параметров, называется силовым полем. Различные реализации молекулярной механики используют слегка отличающиеся математические выражения и, следовательно, различные константы в потенциальной функции. Распространенные силовые поля, используемые в настоящее время, были разработаны с использованием точных квантовых расчетов и/или подгонкой под экспериментальные данные.

Для поиска локального минимума потенциальной энергии используются соответствующие методы минимизации, а для изучения поведения систем с течением времени используются методы молекулярной динамики. Низшие энергетические состояния более стабильны и имеют более важное значение из-за своей роли в химических и биологических процессах. Молекулярно-динамические расчеты, с другой стороны, показывают поведение системы как функцию от времени. И для минимизации, и для молекулярной динамики главным образом используется второй закона Ньютона — F = ma. Интегрирование этого закона движения с помощью различных алгоритмов приводит к получению траекторий атомов в пространстве и времени. Сила, действующая на атом, определяется как отрицательная производная функции потенциальной энергии.

Молекулы могут быть смоделированы как в вакууме, так и в присутствии растворителя, например воды. Расчёты систем в вакууме называются расчётами «в газовой фазе», в то время как расчёты, включающие молекулы растворителя, называются расчётами «с явно заданным растворителем». Другая группа расчётов учитывает наличие растворителя оценочно, с помощью дополнительных членов в потенциальной функции — так называемые расчёты «с неявным растворителем».

В настоящее время методы молекулярного моделирования стали обыденными при изучении структуры, динамики и термодинамики неорганических, биологических и полимерных систем. Среди биологических явлений, которые исследуются методами ММ, сворачивание белков, ферментативный катализ, стабильность белков, конформационные превращения и процессы молекулярного узнавания в белках, ДНК и мембранах.

Просмотров: 12024

<<< Морфолино